
Нехай Ахілл змагається з черепахою, швидкість якої значно менша за швидкість Ахілла. Ахілл починає біг із точки A, а черепаха трохи попереду нього, з точки В. Поки Ахілл добіжить від А до В, черепаха проповзе від В до С. Поки Ахілл добіжить від В до С, черепаха проповзе від С до D, так само і з іншими точками. Отже, Ахілл ніколи не зможе наздогнати черепаху.
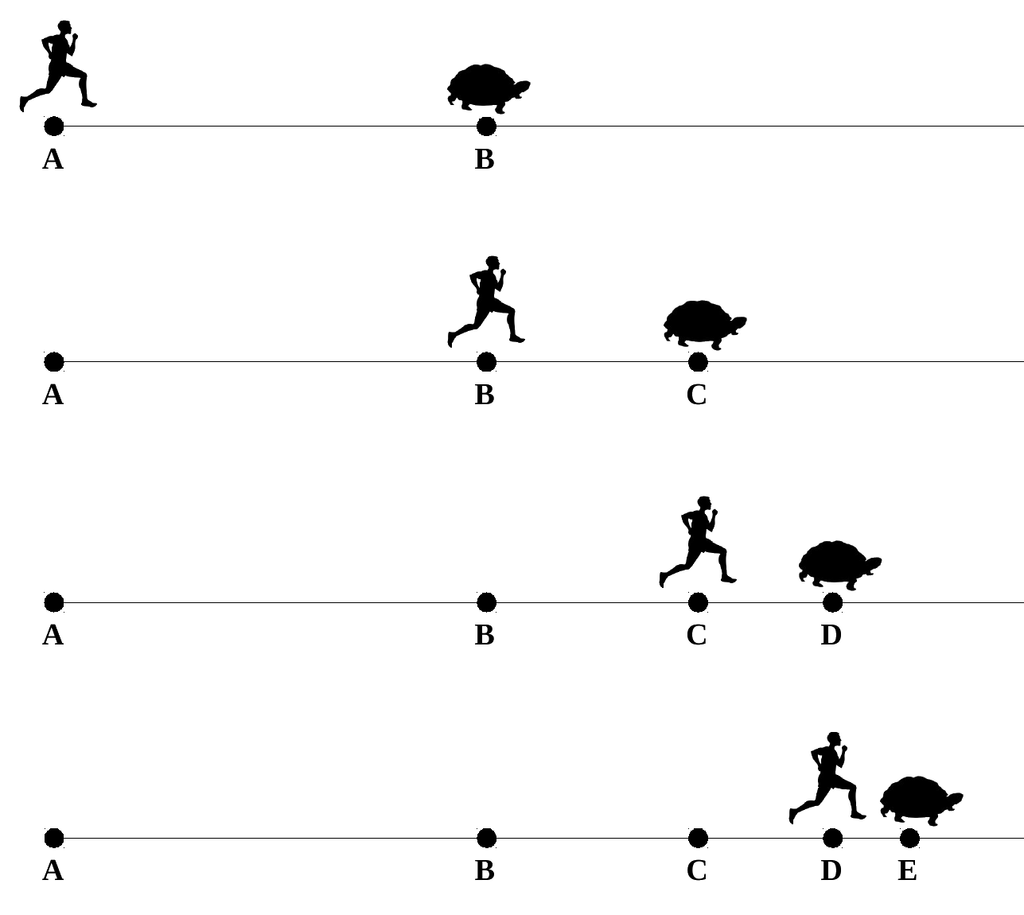
Суперечності в цих двох апоріях виникають із припущення, що час і простір можна ділити нескінченно. Насправді, як би там не було, тут виникає нескінченна спадна геометрична прогресія, а сума не скінченної спадної геометричної прогресії є скінченним числом.
Ще немає коментарів...
© 2026 Веселі задачки. Усі права захищені.