Троє хлопчиків грали в шашки. Усього було зіграно три партії. По скільки партій зіграв кожен хлопчик? Читати далі

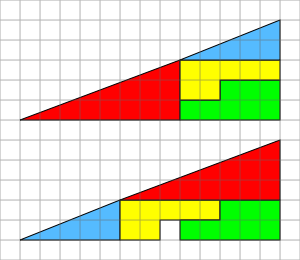
На малюнку зображено дві фігури. Кожна з фігур складається з одних і тих же деталей. Порядок розташування деталей, як відомо, не впливає на загальну площу фігури. Куди пропав квадратик на нижньому малюнку? Читати далі

Є 10 карток. На кожній з них з обох сторін написано по одному натуральному числу: на першій – числа  і , на другій – числа  і , … , на 10-тій – числа 19 і 20. Усі ці картки розташовані в ряд на довгому столі. Двоє гравців грають у таку гру. За один хід гравець довільно обирає п’ять карток і перевертає їх. Програє той гравець, після ходу якого на столі з’явиться розташування чисел, що вже зустрічалося у ході гри (можливо, в початковий момент). Хто має можливість забезпечити собі виграш – той, хто починає гру, чи його суперник? Читати далі

На одній вулиці розташовано 5 будинків різного кольору (синього, білого, жовтого, зеленого і червоного). В цих будинках живе 5 людей різних національнотей (швед, данець, англієць, німець та норвежець), які п’ють 5 різних видів напоїв (пиво, кава, чай, вода, молоко), курять 5 різних марок цигарок(Dunhill, Marlboro, Rothmans, Pall Mall та Phillip Morris) та розводять 5 різних тваринок (коні, птахи, рибки, коти та собаки). Читати далі

Трьом учням в темній кімнаті одягли на голову по чорній шапці. Перед ними поставлено завдання відгадати, хто в якій шапці, якщо всього шапок 5, причому 2 з них – сірі, а 3 – чорні. Сірі шапки сховали перед тим, як у кімнаті запалили світло. Через деякий час один учень відгадав, що він стоїть в чорній шапці. Як він це зробив? Читати далі

Плитка шоколаду складається з 35 квадратиків (7 5). Ламають по прямих, які ділять квадратики до тих пір, поки не одержать окремі 35 квадратиків. Скільки разів потрібно поділити шоколадку? Читати далі

Три розбійника хочуть поділити здобич порівну. Кожен з них упевнений, що тільки він поділить здобич на рівні частини, але інші не мають довіри до нього. Якщо б розбійників було двоє, тоді було б легше вийти з цього становища: один розділив би здобич на 2 частини, а другий взяв би ту частину, яка здавалась йому більшою. Як повинні діяти розбійники, щоб кожен з них був упевнений, що його здобич не менше третьої частини всієї здобичі? Читати далі

Вчитель перевірив роботи трьох учнів – Олексієва, Василенка і Сергієнка, але не приніс у клас. Учням він сказав: “Один із вас отримав “3”, другий – “4”, а третій – “5”. У Сергієнка не “5”, у Василенка не “4”, а у Олексієва, здається, “4”.

Коли принесли зошити, то виявилось, що вчитель тільки одному учневі сказав правильну оцінку, двом іншим – неправильну. Які оцінки отримали учні? Читати далі

Кожен із трьох друзів зіграв однакову кількість шахових партій з іншим. При цьому вияснилось, що перший з них виграв найбільшу кількість партій, другий програв найменшу кількість партій, а третій набрав найбільшу кількість очків. Чи могло так бути? Якщо ні, то доведіть. Якщо так, то наведіть приклад. Читати далі

Маємо 2 купи каміння. Гра складається з того, що кожен із двох гравців по черзі забирає будь-яку кількість камінців тільки з однієї купи. Виграє той, хто бере останнім. Знайти спосіб гри, який забезпечує виграш тому гравцеві, який може або розпочати гру, або надати перший хід своєму партнеру. Читати далі