Лупа

Що не може збільшити лупа в трикутнику? Читати далі

Що не може збільшити лупа в трикутнику? Читати далі

У кімнаті горіло 50 свічок, 20 із них загасили. Скільки залишиться? Читати далі
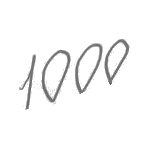
Як, не відриваючи олівця від паперу, написати цифрами 1000 так, щоб всі цифри були написані окремо один від одного? Читати далі

Ковалю принесли п’ять ланцюгів, по три кільця в кожному, і доручили з’єднати їх в один ланцюг. Коваль вирішив розкрити чотири кільця й знову їх закувати. Чи не можна виконати ту ж роботу, розкривши менше кілець?
Відповідь:
[hidepost]Розкрити три кільця одного ланцюга, а потім цими кільцями з’єднати чотири шматки, що залишилися.[/hidepost]

Василю, Петру, Семену і їхнім дружинам Наталії, Ірині, Ганні разом 151 рік. Кожен чоловік старше своєї дружини на 5 років. Василь на 1 рік старше Ірини. Наталії й Василю разом 48 років, Семену й Наталії разом 52 роки. Хто на кому одружений, скільки кому років? (Вік повинен бути виражений в цілих числах.) Читати далі

Три брати, повертаючись з театру додому, підійшли до зупинки трамвая, щоб ускочити в перший же вагон, який підійде. Вагон не з’являвся, і старший брат запропонував почекати.
– Ніж стояти тут і чекати, – відповів середній брат, – краще підемо вперед. Коли який-небудь вагон наздожене нас, тоді й ускочимо; а тим часом хоч би частина дороги буде вже за нами – швидше додому приїдемо. Читати далі

Колгоспниця принесла на базар качани капусти і продала трьом покупницям. Перша взяла половину всіх качанів і ще півкапустини. Друга купила половину качанів, що залишились і ще півкапустини. Третя покупниця взяла останній качан.
Скільки качанів капусти винесла на базар колгоспниця? Читати далі

Троє хлопчиків грали в шашки. Усього було зіграно три партії. По скільки партій зіграв кожен хлопчик? Читати далі
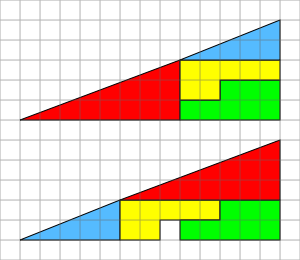
На малюнку зображено дві фігури. Кожна з фігур складається з одних і тих же деталей. Порядок розташування деталей, як відомо, не впливає на загальну площу фігури. Куди пропав квадратик на нижньому малюнку? Читати далі

Є 10 карток. На кожній з них з обох сторін написано по одному натуральному числу: на першій – числа і , на другій – числа і , … , на 10-тій – числа 19 і 20. Усі ці картки розташовані в ряд на довгому столі. Двоє гравців грають у таку гру. За один хід гравець довільно обирає п’ять карток і перевертає їх. Програє той гравець, після ходу якого на столі з’явиться розташування чисел, що вже зустрічалося у ході гри (можливо, в початковий момент). Хто має можливість забезпечити собі виграш – той, хто починає гру, чи його суперник? Читати далі